In this video I explain the concept of kurtosis. I explain the terminology for kurtosis coined by Karl Pearson, a number of common misconceptions related to kurtosis, how kurtosis is calculated for a sample, and how kurtosis is interpreted for assumptions about normality and the detection of outliers.
DeCarlo (1997) On the Meaning and Use of Kurtosis http://www.columbia.edu/~ld208/psymeth97.pdf
Westfall (2014) Kurtosis as Peakedness; 1905-2014 R.I.P https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4321753/
Video Transcript
Hi, I’m Michael Corayer and this is Psych Exam Review. In the videos on skew we looked at one way that a distribution can differ from a normal distribution and this was in terms of symmetry. So a normal distribution is perfectly symmetrical but a distribution could be asymmetrical and have positive or negative skew.
Now we’re going to look at another way that a distribution can differ from normality and this is in terms of the heaviness of its tails. So a distribution can have heavier or lighter tails compared to a normal distribution and this will give it what’s called positive or negative kurtosis.
Now kurtosis is not emphasized in most introductory courses and part of the reason for this is that it’s very hard to judge visually, especially without any direct comparison to a normal curve, and this can make it feel somewhat vague. It’s also the case that there’s a number of misconceptions about kurtosis and these can also lead to some confusion.
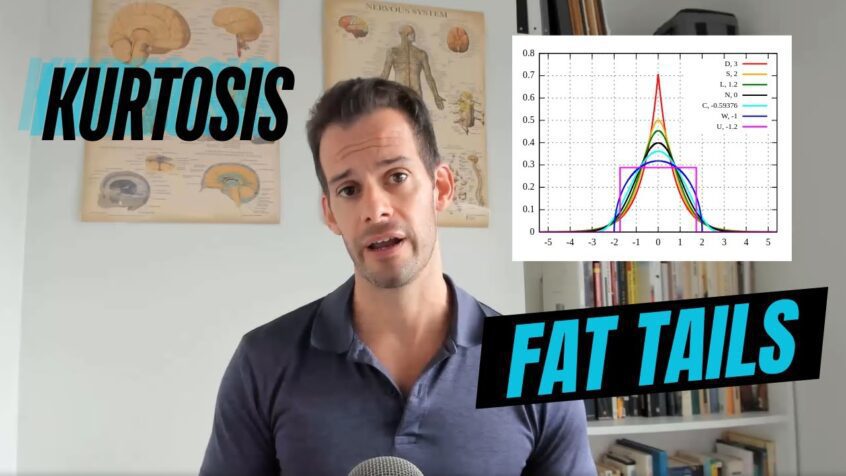
So let’s start by getting a sense of what I mean by the tails of the distribution. We can think of a distribution as having three sections; we have the center or the peak and this refers to scores that fall less than a standard deviation away from the mean. And then we move to what we can call the shoulders of the distribution, and this would refer to scores that fall around one standard deviation away from the mean on either side. And then lastly we have the tails and this would refer to the scores that fall more than a standard deviation away from the mean. So now that have a sense of these different parts of a distribution, we can look at some of the somewhat misleading terminology that’s used to talk about kurtosis.
So let’s look at some of the basic terms for talking about kurtosis and these were coined by Karl Pearson in 1905. And we can start with kyrtos and this is where we get kurtosis, and this is the Greek for curved or bulging or convex. And what we’ll see is we have three different prefixes that we can attach to this; we have lepto, meso, and platy. And so if we have a mesokurtic distribution, meso comes from the word for middle, and so this is sort of our middle comparison point. And this is because a normal curve is an example of a mesokurtic distribution. And if we look at its sort of raw kurtosis score we’ll get a value of three and so what we’re going to do to make this our point of comparison is when we calculate the kurtosis, we’re really looking for what we can call the “excess kurtosis”. We want to see, how much does it differ from 3? And so later when we look at the formula we’ll see we’re going to calculate the kurtosis and then we’re going to subtract 3 from it, in order to make a comparison to a normal distribution. And so we have two ways we can vary; we could have more kurtosis than a normal distribution, or we could have less kurtosis than a normal distribution.
Now if we have more kurtosis than a normal distribution this is where we’re going to use this term lepto. So lepto comes from the Greek for “thin”. Now it’s not commonly used in other English words but you might see it if you think of the hormone leptin. This is a hormone that signals satiety and reduces the hunger signal, but the thinness here is referring to the peak of the distribution. And as we’re going to see this is really not a good way to name this, right? This is part of the reason we have some misconceptions. What we should focus on instead when we look at a leptokurtic distribution or positive kurtosis.
So if we look at this diagram here that solid line is the leptokurtic distribution and the dotted line is the normal distribution, and what we see is if we look at the tails, we have heavier tails in the leptokurtic distribution, right? There’s more score values here than there would be if it were a normal curve. And this is really what’s going to be driving this positive kurtosis.
On the other hand we could have a distribution that has less kurtosis compared to a normal curve and this would be a platykurtic distribution. Now platy comes from the Greek for flat and this you do see in English in words like plateau, plate, you see it in platypus “flat foot” and you see it in other languages like in Spanish. If you know plata for silver, which might seem strange but Spanish silver was pressed into flat plates. And you may also know plata if you watched Narcos and you’re familiar with Pablo Escobar’s famous phrase “plata o plomo”; silver or lead, meaning the choice between money or a bullet. In any case when we look at a platykurtic distribution in this sort of stylized picture here we see it does have this flat center, but as I said that’s kind of misleading. What we should focus on instead is the tails. And what we see, again, is in this case we have lighter tails compared to a normal distribution, right? This solid line here is not extending out as far, right? It has lighter tails; they’re sort of cut off here. And so we’d see more extreme scores in a normal distribution than we would see in a platykurtic distribution, and this is why it’s going to have a kurtosis value that’s lower than 3. And so when we subtract 3 we’re going to get a negative value. And so a platykurtic distribution is going to be an example of negative kurtosis.
So we can also see with these terms that these are part of the source of the confusion about kurtosis, because they cause us to focus on the wrong part of the distribution. They make us think about thinness and flatness and we start thinking about the center of the distribution, when in fact what we should be focusing on is the tails of the distribution. And we’ll see why later when we look at the formula for kurtosis.
Three common misconceptions about kurtosis were described in a paper by Lawrence DeCarlo in 1997 titled “On the Meaning and Use of Kurtosis” and I’ll post a link in the video description box to the paper if you’d like to read it. The first misconception that DeCarlo pointed out was some sources defining kurtosis as being about peakedness alone. The second misconception was that kurtosis was about the relationship between the peak and the tails. And the third misconception related to illustrations of kurtosis where they’d show kurtosis of different distributions but these distributions wouldn’t have the same variance. And so they weren’t clearly showing the difference only in kurtosis because two distributions can differ in their kurtosis even when they have the same variance.
A later paper in 2014 by Peter H. Westfall essentially argued that DeCarlo didn’t go far enough, particularly in his first misconception. So DeCarlo said that we shouldn’t define kurtosis as peakedness alone, but what Westfall said is actually we shouldn’t define kurtosis as being about peakedness at all. The peak or the center of the distribution is essentially irrelevant to the calculation of kurtosis. And this is why he titled this paper “Kurtosis as Peakedness; 1905 to 2014 R.I.P.” and I’ll post a link to this paper in the video description box as well.
So if you have a textbook or other resources that are from prior to 2014 you might see greater emphasis on peakedness when explaining ketosis. But since this paper most sources have conceded that Westfall is right and heavier tails are really what drives a higher kurtosis value and lower kurtosis is the result of thinner tails and that it really doesn’t have much of anything to do with the peak of the distribution. And so in order to understand why this is, we’ll take a look at the formula for kurtosis and we’ll see how it is that Westfall was able to put this idea of kurtosis as peakedness to rest.
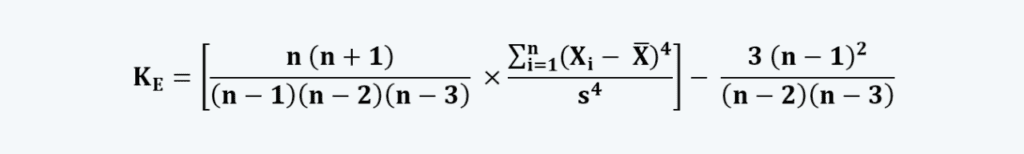
So if you’re using SAS, Minitab, SPSS, or Excel to calculate the kurtosis for a sample, this is the equation that it’s going to be using. Now this looks like a lot but we can break this down into three main parts. In the middle here what we’re doing is we’re finding the standardized fourth moment, and then we’re adjusting it based on our sample size, and finally we’re subtracting 3 in order to compare it to the kurtosis of a normal distribution, but we also have to adjust this based on our sample size. So these three parts together here are going to give us our excess kurtosis in comparison to the kurtosis of a normal curve of the same sample size.
Now we can think about how different parts of the distribution are going to contribute to this calculation. So we can think about those parts we talked about earlier; the peak or the center, the shoulders, and the tails. So let’s start with the shoulders. These are scores that are about a standard deviation away from the mean. Now if we look at the standardized fourth moment we see we’re taking a score’s deviation from the mean and we’re taking that to the fourth power and we’re dividing it by the standard deviation to the fourth power. And so what we’ll see is if we have have a score that’s about one standard deviation away from the mean and we’re dividing by the standard deviation, then that’s going to give us a value of 1. And when we take 1 to the fourth power we’re still going to get a value of 1.
Now we can think about how scores at the peak or the tails are going to contribute. So if we think about scores at the peak or the center of the distribution, then these are scores that are less than a standard deviation away. And so what that means is when we take their deviation from the mean and divide by the standard deviation we’re always going to get a value less than 1. And then when we take that to the fourth power we see that it’s going to become very very small. So if we had a score that’s half a standard deviation away from the mean and we take that to the fourth power, we’re going to get .0625 and so we see these scores at the peak are going to add very little. And scores that were even closer to the mean would add even less than this. And so all of these scores in the peak really aren’t able to contribute very much to our overall calculation of the kurtosis, and this is why we can say that kurtosis is really not about peakedness. Instead it’s about the tails.
So now we can think about scores at the tails. So these are scores that are greater than a standard deviation away from the mean. So if we think about a score here that’s farther from the mean than the standard deviation then we can think about taking that to the fourth power, and we see the values are going to get very large. So if we had a score that was 2 standard deviations away from the mean and then we’re taking that to the fourth powe,r then we see that what that’s going to do is that’s going to add 16 to our calculation. And if we think about a score further out in the tails, maybe 3 standard deviations from the mean, when we take that to the fourth power we’re going to add 81 to our calculation.
And so now we can see that it really is the tails that are driving this calculation of kurtosis, right? These are the scores that matter. If we have fat tails or heavy tails, that means we’re going to have a lot of these higher values and we’re going to end up with greater kurtosis, regardless of what’s happening at the peak or the center, because those scores just aren’t able to contribute very much to the calculation. And in contrast if we have very light or thin tails, then our kurtosis value is going to be much lower, regardless of what’s happening at the peak, right? So that’s going to give us negative kurtosis. And so we can see that this calculation of kurtosis is really just about the heaviness or the lightness of the tails of our distribution.
So how can we interpret kurtosis? In most introductory statistics courses you won’t go into detail on kurtosis and so for now what we’ll say is we can think about skew and kurtosis as being two main ways of thinking about how our distribution might differ from a normal distribution. And that’s going to be useful when we think about the types of tests or the types of analyses that we can do on that data, depending on the assumptions of normality that are inherent to those tests. Now another thing we can say about kurtosis is it can be useful for helping us to detect outliers. This is because if we have more outliers then that’s going to increase our kurtosis. And so if we had a normal distribution and then we just added some outliers to it, what we’d see is it would now have positive ketosis. And so that positive ketosis might be an indication that our distribution has outliers.
So hopefully this clarified what ketosis is, and maybe more importantly, what it isn’t, and dispelled some of the common misconceptions that you might see related to ketosis. Let me know in the comments if this was helpful for you or if there’s questions that you still have and I’ll try my best to answer them. Don’t forget to like and subscribe, and be sure to check out the hundreds of other psychology and statistics tutorials that I have on this channel, which are also organized into playlists by unit. As always, thanks for watching!